博客
关于我
强烈建议你试试无所不能的chatGPT，快点击我
平衡二叉树(AVL)的理解和实现(Java)
阅读量：4341 次
发布时间：2019-06-07

本文共 17791 字，大约阅读时间需要 59 分钟。

AVL的定义

平衡二叉树：是一种特殊的，其中每一个节点的左子树和右子树的高度差至多等于1。从平衡二叉树的名字中可以看出来，它是一种高度平衡的二叉排序树。那么什么叫做高度平衡呢？意思就是要么它是一颗空树，要么它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度只差的绝对值绝对不超过1。

平衡因子：将二叉树上节点的左子树深度减去右子树深度的值称为平衡因子BF。则平衡二叉树上所有节点的平衡因子只可能是1，-1，0。
只要二叉树上有一个节点的平衡因子的绝对值大于1，那么该二叉树就是不平衡的。
最小不平衡子树：距离插入节点最近的，且平衡因子的绝对值大于1的节点为根的子树，我们称之为最小不平衡子树。

平衡二叉树实现原理

平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个节点时，先检查是否因插入而破坏了树的平衡性，若是，找出最小不平衡树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各节点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。

旋转操作：
  • 右旋：最小不平衡子树的BF和它的子树BF符号相同且最小不平衡子树的BF大于0
  • 左旋：最小不平衡子树的BF和它的子树BF符号相同且最小不平衡子树的BF小于零
  • 左右旋：最小不平衡子树的BF与它的子树的BF符号相反时且最小不平衡子树的BF大于0时，需要对节点先进行一次向左旋使得符号相同后，在向右旋转一次完成平衡操作。
  • 右左旋：最小不平衡子树的BF与它的子树的BF符号相反时且最小不平衡子树的BF小于0时，需要对节点先进行一次向右旋转使得符号相同时，在向左旋转一次完成平衡操作。

放一张自己理解的图：

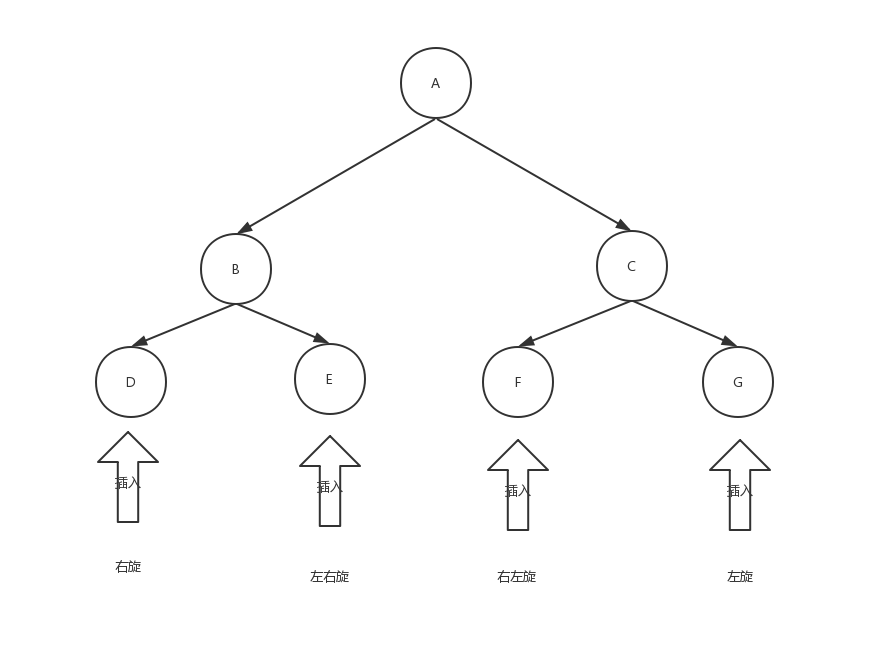
在这里插入图片描述

平衡二叉树的构建

节点定义

平衡二叉树节点数据结构和二叉排序树相差不大：

public class AVLNode {
    	public AVLNode parent;	public AVLNode leftChild, rightChild;	public int data;		public AVLNode(AVLNode parent, AVLNode leftChild, AVLNode rightChild, int data) {
    		this.parent = parent;		this.leftChild = leftChild;		this.rightChild = rightChild;		this.data = data;	}		public AVLNode(int data) {
    		this(null, null, null, data);	}		public AVLNode(AVLNode parent, int data) {
    		this.parent = parent;		this.data = data;	}}
插入节点

在进行插入时，我们需要考虑插入的这个节点会不会破坏二叉树的平衡，如果平衡被打破，那么我们需要考虑如何调整二叉树的结构使得平衡恢复。

我们以插入后左子树比右子树BF大2的所有情况举例，下面的图只是代表着那个被打破平衡的点的子树，并不代表整棵树。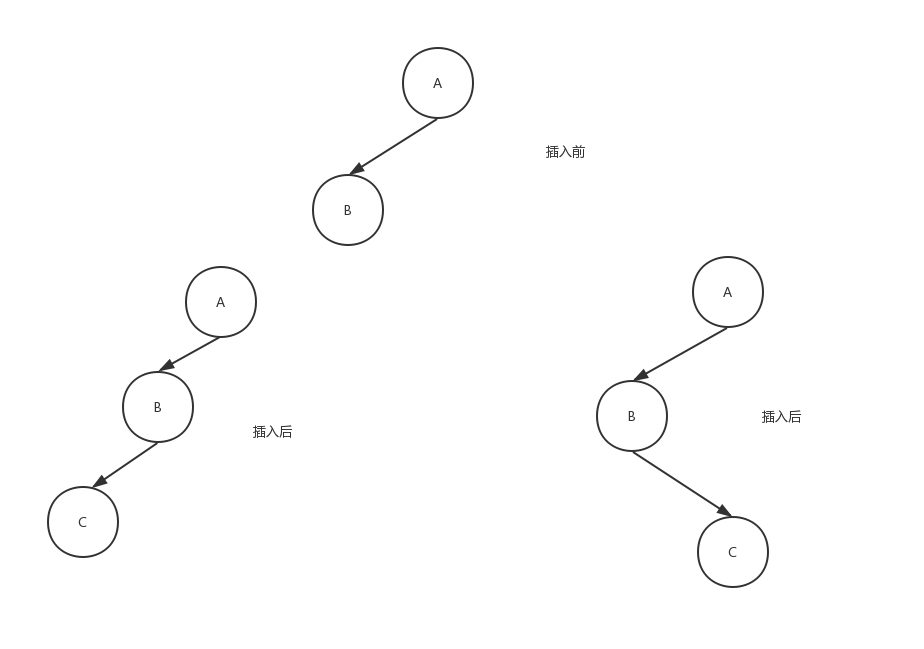
在这里插入图片描述
这是第一种情况，其中A和B节点是平衡二叉树树中某一节点集合，现在插入C，可以从图上看到，要想打破平衡，节点C必须插入B上
第二种情况：
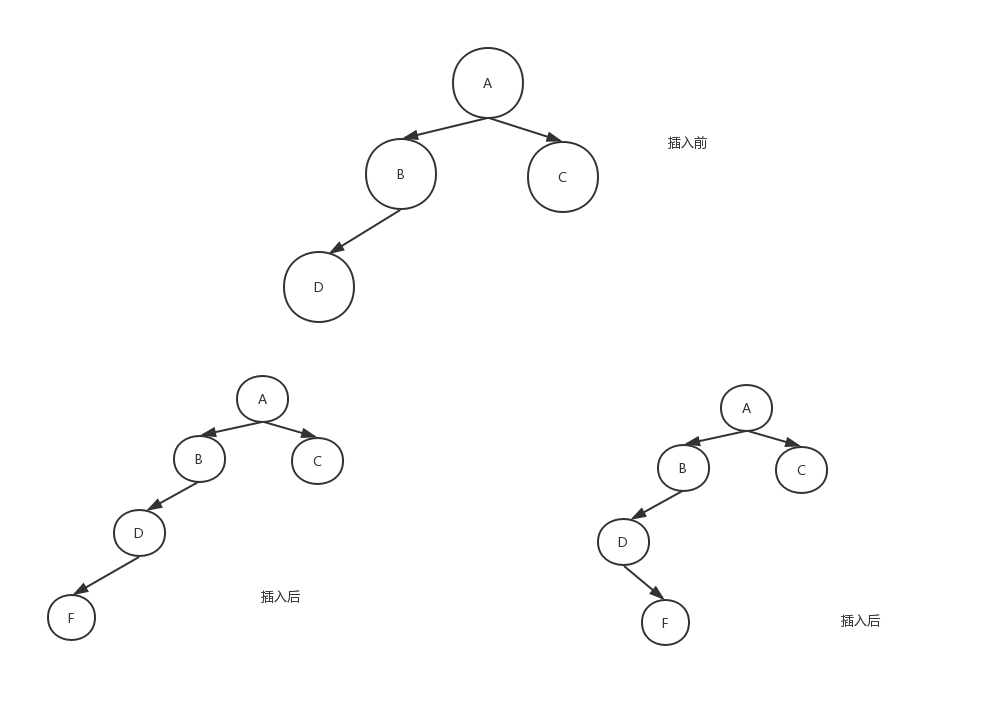在这里插入图片描述
其中的A、B、C、D是平衡二叉树中某一节点集合，现在插入节点F，平衡被打破，那么F需要插入到D上才能打破平衡。
第三种情况：
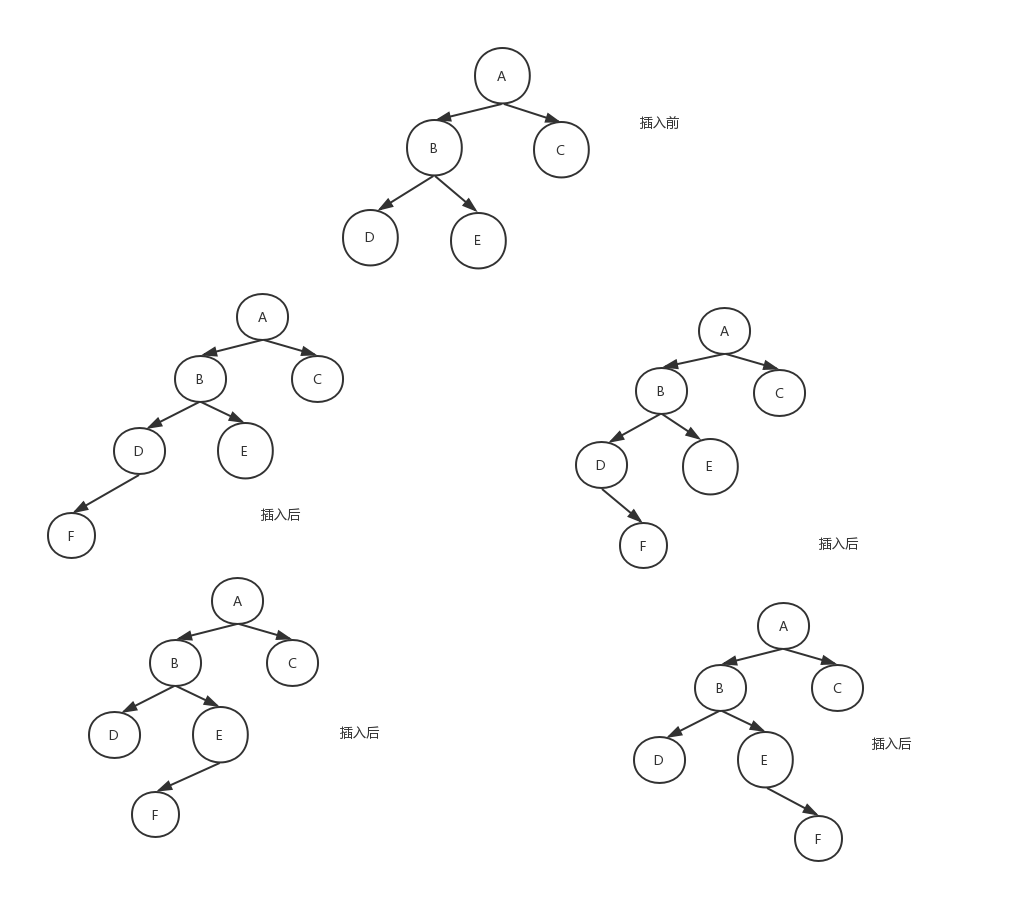在这里插入图片描述
其中A、B、Ｃ、Ｄ、Ｅ为平衡二叉树中某一节点集合，并不表示整棵树。现在插入F节点，平衡被打破，那么F只能插在D、Ｅ上。
通过观察发现第二、三中情况其实是第一种情况衍变而来，如分别在A节点和B节点上增加节点就变成了第二三中情况。
对于第一种情况进行研究：
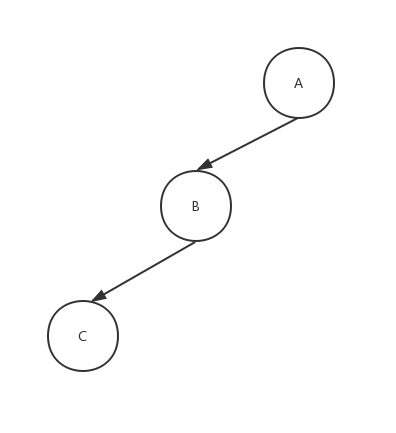在这里插入图片描述
要使A节点的BF小于2，我们需要对该节点集合的结构进行相应调整，根据二叉排序树的性质我们知道A节点的值一定比B节点大，而C节点的值一定比B节点的大，所以我们可以将B节点来替换A节点，让A节点做B节点的右孩子。若A节点有父节点，那么A的父节点的子节点要指向B节点，同时A节点的父节点为B，也就是进行右旋操作：
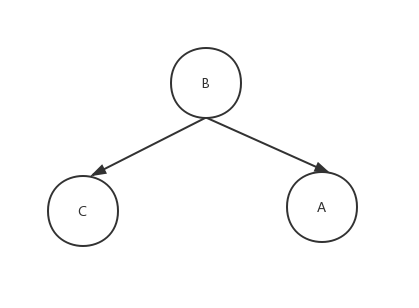在这里插入图片描述
而对于第一种情况的这种图：
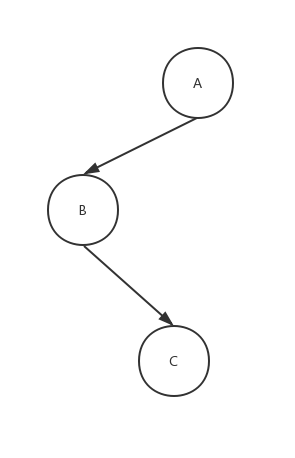在这里插入图片描述
我们发现使用上面的逻辑好像并不能完成平衡，执行完之后是这样子的：
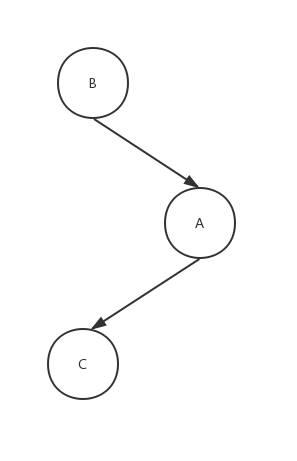在这里插入图片描述
这样子根本没有平衡。所以不能仅旋转一次。我们发现对于A节点它的BF等于2，对于B节点它的BF值等于-1，符号相反，所以我们需要执行左右旋，先将最小不平衡子树和它的子树的BF符号相同，在进行平衡。
对于B节点执行左旋，那么C节点会变成A节点的左子节点，同时B节点会变成C节点的左子节点，这样就又回到了最初的情况：
在这里插入图片描述
在执行右旋，完成平衡化：在这里插入图片描述
对于第二种情况和第三种情况实际上分析思路和第一种情况一样。
右旋代码：

/**	 * 右旋	 * @param node	 * @return	 */	public AVLNode rightRotation(AVLNode node) {
    		if(node != null) {
    						AVLNode leftChild = node.leftChild;			node.leftChild = leftChild.rightChild;			// 如果leftChild的右节点存在，则需将该右节点的父节点指给node节点			if(leftChild.rightChild != null) {
      				leftChild.rightChild.parent = node;			}			leftChild.parent = node.parent;			if(node.parent == null) {
    				this.root = leftChild;			}			else if(node.parent.rightChild == node) {
      // 即node节点在它原父节点的右子树中				node.parent.rightChild = leftChild;			}			else if(node.parent.leftChild == node) {
    				node.parent.leftChild = leftChild;			}						leftChild.rightChild = node;			node.parent = leftChild;			return leftChild;		}				return null;	}

左旋代码：

/**	 * 左旋	 * @param node	 * @return	 */	public AVLNode leftRotation(AVLNode node) {
    				if(node != null) {
    			AVLNode rightChild = node.rightChild;			node.rightChild = rightChild.leftChild;			if(rightChild.leftChild != null) {
    				rightChild.leftChild.parent = node;			}			rightChild.parent = node.parent;			if(node.parent == null) {
    				this.root = rightChild;			}			else if(node.parent.rightChild == node) {
    				node.parent.rightChild = rightChild;			}			else if(node.parent.leftChild == node) {
    				node.parent.leftChild = rightChild;			}			rightChild.leftChild = node;			node.parent = rightChild;			return rightChild;		}				return null;	}

那么现在有一个问题，怎么判别被打破的平衡要经历哪种操作才能达到平衡呢？

根据上面的原理，分为四种情况，这四种情况可以划分为两大类：

  • 第一大类，A节点的左子树高度比右子树高度高2，最终需要经过右旋操作(可能需要先左后右)
  • 第二大类，A节点的左子树高度比右子树高度低2，最终需要经过左旋操作(可能需要先右后左)

所以我们插入新节点的思路就是，在插入节点之后，判断插入的节点是在A的左子树还是右子树。

插入节点代码：

/**	 * 插入节点	 * @param data	 */	public void put(int data) {
    		putData(root, data);	}		private boolean putData(AVLNode node, int data) {
    		if(node == null) {
    			node  = new AVLNode(data);			root = node;			return true;		}		int t;		AVLNode p;		AVLNode temp = node;		do {
    			p = temp;			t = temp.data - data;			if(t < 0) {
    				temp = temp.rightChild;			}			else if(t > 0) {
    				temp = temp.leftChild;			}			else {
    				return false;			}		} while(temp != null);				if(t < 0) {
    			p.rightChild = new AVLNode(p, data);		}		else if(t > 0) {
    			p.leftChild = new AVLNode(p, data);		}		rebuild(p); //平衡二叉树的方法		return true;			}

对于rebuild()方法：

/**	 * 平衡二叉树的方法	 * @param node	 */	public void rebuild(AVLNode node) {
    		while(node != null) {
    			if(calcNodeBalanceValue(node) == MAX_LEFT) {
    　//左子树高				fixAfterInsertion(node, LEFT);			}			else if(calcNodeBalanceValue(node) == MAX_RIGHT) {
    　//右子树高				fixAfterInsertion(node, RIGHT);			}			node = node.parent;		}	}

这段代码从插入节点的父节点开始，向上回朔的去查找失去平衡的节点，通过calcNodeBalanceValue()方法来结算当前节点的左右子树高度差，判断是2(MAX_LEFT)还是-2(MAX_RIGHT)。

计算节点BF的相应方法：

/**	 * 计算node节点的BF值	 * @param node	 * @return	 */	public int calcNodeBalanceValue(AVLNode node) {
    		if(node != null) {
    			return getHeightByNode(node);		}		return 0;	}		private int getHeightByNode(AVLNode node) {
    		if(node == null) {
    			return 0;		}		return getChildDepth(node.leftChild) - getChildDepth(node.rightChild);	}		private int getChildDepth(AVLNode node) {
    		if(node == null) {
    			return 0;		}		return 1 + Math.max(getChildDepth(node.leftChild), getChildDepth(node.rightChild));	}

在找到相应的类型后，执行fixAfterInsertion()来完成对不同类型的调整方法。

/**	 * 调整树的结构	 * @param node	 * @param type	 */	public void fixAfterInsertion(AVLNode node, int type) {
    		if(type == LEFT) {
    			AVLNode leftChild = node.leftChild;			if(leftChild.leftChild != null) {
      //右旋				rightRotation(node);			}			else if(leftChild.rightChild != null) {
       //左右旋				leftRotation(leftChild);				rightRotation(node);			}		}		else if(type == RIGHT) {
    			AVLNode rightChild = node.rightChild;			if(rightChild.rightChild != null) {
       //左旋				leftRotation(node);			}			else if(rightChild.leftChild != null) {
       //右左旋				rightRotation(rightChild);				leftRotation(node);			}		}	}

根据我参考其他博主的想法，通过左右子树是否为空的判断来决定它是单旋还是双旋，原因：如果代码执行到了这个方法，那么肯定平衡被打破了，就暂且拿第一个大类来说 ，A的左子树高度要比右子树高2，意味平衡被打破了，再去结合上面分析的第一种情况，当插入元素后树结构是以下结构，那肯定是单旋。

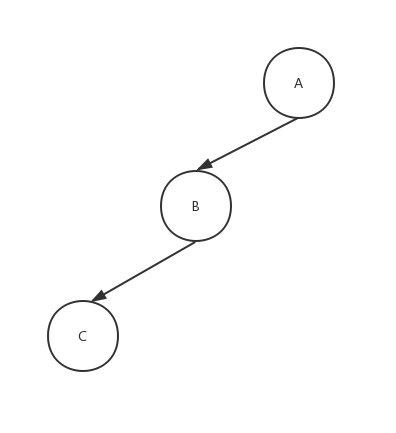在这里插入图片描述
如果是以下结构，那肯定是这种结构，由上面分析，这种结构必须的双旋。
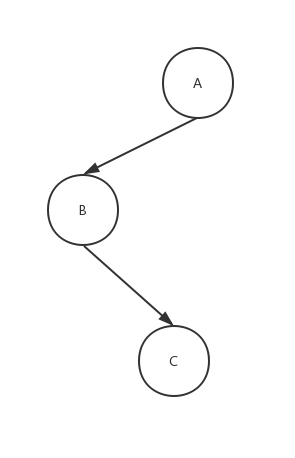在这里插入图片描述
所以，这里是根据插入的节点是位于B节点的左右方来决定是单旋还是双旋(在这里，不保证结论完全正确，若有错误，还望大家指正)。
以上是对平衡二叉树的插入操作和平衡话操作。

中序遍历：

对于平衡二叉树和二叉排序树的遍历是相同的，因为平衡二叉树就是一个特殊的二叉排序树。

/**	 * 中序遍历	 */	public void middOrderErgodic() {
    		this.middOrderErgodic(this.root);	}	public void middOrderErgodic(AVLNode node) {
    		if(node != null) {
    			this.middOrderErgodic(node.leftChild);			System.out.print(node.data + ", ");			this.middOrderErgodic(node.rightChild);		}	}
根据key值获得指定的节点：
/**	 * 获得指定节点	 * @param key	 * @return	 */	public AVLNode getNode(int key) {
    			AVLNode node = root;		int t;		do {
    			t = node.data - key;			if(t > 0) {
    				node = node.leftChild;			}			else if(t < 0) {
    				node = node.rightChild;			}			else {
    				return node;			}		} while(node != null);		return null;	}
对平衡二叉树进行层序遍历：
/**	 * 层序遍历	 */	public void sequenceErgodic() {
    		if(this.root == null) {
    			return;		}		Queue
    
      queue = new LinkedList<>();		AVLNode temp = null;		queue.add(this.root);		while(!queue.isEmpty()) {
    			temp = queue.poll();			System.out.println("当前节点值：" + temp.data + ", BF：" + calcNodeBalanceValue(temp));			if(temp.leftChild != null) {
    				queue.add(temp.leftChild);			}			if(temp.rightChild != null) {
    				queue.add(temp.rightChild);			}		}	}

采用队列，将一层所有的节点保存在一个队列中，并按序输出。

获得平衡二叉树指定节点的后继：
/***	 * 获得指定节点的后继	 * 找到node节点的后继节点     * 1、先判断该节点有没有右子树，如果有，则从右节点的左子树中寻找后继节点，没有则进行下一步     * 2、查找该节点的父节点，若该父节点的右节点等于该节点，则继续寻找父节点，     *   直至父节点为Null或找到不等于该节点的右节点。     * 理由:     *      后继节点一定比该节点大，若存在右子树，则后继节点一定存在右子树中，这是第一步的理由     *      若不存在右子树，则也可能存在该节点的某个祖父节点(即该节点的父节点，或更上层父节点)的右子树中，     *      对其迭代查找，若有，则返回该节点，没有则返回null	 * @param node	 * @return	 */	public AVLNode getSuccessor(AVLNode node) {
    		if(node.rightChild != null) {
    			AVLNode rightChild=  node.rightChild;			while(rightChild.leftChild != null) {
    				rightChild = rightChild.leftChild;			}			return rightChild;		}		AVLNode parent = node.parent;		while(parent != null && (node == parent.rightChild)) {
    			node = parent;			parent = parent.parent;		}		return parent;	}

这里的思想我也是看了半天，首先我们对于节点后继应该是在该节点右子树中最小的值，但是因为在插入时结构进行了调整，节点后继不在该节点右子树中，那么这时应该查找该节点的父节点，若该父节点的右节点等于该节点，则继续寻找父节点，直至父节点为Null或找到不等于该节点的右节点。

删除节点

要注意的是，需要删除节点后的二叉树检测是否有平衡打破的问题，如果平衡被打破，应该重新跳转当前二叉树结构，以恢复平衡化

/**	 * 删除指定val值的节点	 * @param val	 * @return	 */	public boolean delete(int val) {
    		AVLNode node = getNode(val);		if(node == null) {
    			return false;		}		boolean flag = false;		AVLNode p = null;		AVLNode parent = node.parent;		AVLNode leftChild = node.leftChild;		AVLNode rightChild = node.rightChild;		if(leftChild == null && rightChild == null) {
    			if(parent != null) {
    				if(parent.leftChild == node) {
    					parent.leftChild = null;				}				else if(parent.rightChild == node) {
    					parent.rightChild = null;				}			}			else {
    				this.root = null;			}						p = parent;			node = null;			flag = true;		}		else if(leftChild == null && rightChild != null) {
    			if(parent != null && parent.data > val) {
    				parent.leftChild = rightChild;			}			else if(parent != null && parent.data < val) {
    				parent.rightChild = rightChild;			}			else {
    				this.root = rightChild;			}			p = parent;			node = null;			flag = true;		}		else if(leftChild != null && rightChild == null) {
    			if(parent != null &&  parent.data > val) {
    				parent.leftChild = leftChild;			}			else if(parent != null && parent.data < val) {
    				parent.rightChild = leftChild;			}			else {
    				this.root = leftChild;			}						p = parent;			node = null;			flag = true;		}		else if(leftChild != null && rightChild != null) {
    			AVLNode successor = getSuccessor(node);			int tempData = successor.data;			if(delete(tempData)) {
    				node.data = tempData;			}			p = successor;			successor = null;			flag = true;		}				if(flag) {
    			this.rebuild(p);		}		return flag;		}

完整代码

package 平衡二叉树;import java.util.LinkedList;import java.util.Queue;public class MyAVLTree {
    	private AVLNode root;	private final int LEFT = 1;	private final int RIGHT = -1;	private final int MAX_LEFT = 2;	private final int MAX_RIGHT = -2;		/**	 * 插入节点	 * @param data	 */	public void put(int data) {
    		putData(root, data);	}		private boolean putData(AVLNode node, int data) {
    		if(node == null) {
    			node  = new AVLNode(data);			root = node;			return true;		}		int t;		AVLNode p;		AVLNode temp = node;		do {
    			p = temp;			t = temp.data - data;			if(t < 0) {
    				temp = temp.rightChild;			}			else if(t > 0) {
    				temp = temp.leftChild;			}			else {
    				return false;			}		} while(temp != null);				if(t < 0) {
    			p.rightChild = new AVLNode(p, data);		}		else if(t > 0) {
    			p.leftChild = new AVLNode(p, data);		}		rebuild(p);		return true;			}		/**	 * 平衡二叉树的方法	 * @param node	 */	public void rebuild(AVLNode node) {
    		while(node != null) {
    			if(calcNodeBalanceValue(node) == MAX_LEFT) {
    				fixAfterInsertion(node, LEFT);			}			else if(calcNodeBalanceValue(node) == MAX_RIGHT) {
    				fixAfterInsertion(node, RIGHT);			}			node = node.parent;		}	}			/**	 * 调整树的结构	 * @param node	 * @param type	 */	public void fixAfterInsertion(AVLNode node, int type) {
    		if(type == LEFT) {
    			AVLNode leftChild = node.leftChild;			if(leftChild.leftChild != null) {
      //右旋				rightRotation(node);			}			else if(leftChild.rightChild != null) {
       //左右旋				leftRotation(leftChild);				rightRotation(node);			}		}		else if(type == RIGHT) {
    			AVLNode rightChild = node.rightChild;			if(rightChild.rightChild != null) {
       //左旋				leftRotation(node);			}			else if(rightChild.leftChild != null) {
       //右左旋				rightRotation(rightChild);				leftRotation(node);			}		}	}			/**	 * 右旋	 * @param node	 * @return	 */	public AVLNode rightRotation(AVLNode node) {
    		if(node != null) {
    						AVLNode leftChild = node.leftChild;			node.leftChild = leftChild.rightChild;			// 如果leftChild的右节点存在，则需将该右节点的父节点指给node节点			if(leftChild.rightChild != null) {
      				leftChild.rightChild.parent = node;			}			leftChild.parent = node.parent;			if(node.parent == null) {
    				this.root = leftChild;			}			else if(node.parent.rightChild == node) {
      // 即node节点在它原父节点的右子树中				node.parent.rightChild = leftChild;			}			else if(node.parent.leftChild == node) {
    				node.parent.leftChild = leftChild;			}						leftChild.rightChild = node;			node.parent = leftChild;			return leftChild;		}				return null;	}		/**	 * 左旋	 * @param node	 * @return	 */	public AVLNode leftRotation(AVLNode node) {
    				if(node != null) {
    			AVLNode rightChild = node.rightChild;			node.rightChild = rightChild.leftChild;			if(rightChild.leftChild != null) {
    				rightChild.leftChild.parent = node;			}			rightChild.parent = node.parent;			if(node.parent == null) {
    				this.root = rightChild;			}			else if(node.parent.rightChild == node) {
    				node.parent.rightChild = rightChild;			}			else if(node.parent.leftChild == node) {
    				node.parent.leftChild = rightChild;			}			rightChild.leftChild = node;			node.parent = rightChild;			return rightChild;		}				return null;	}		/**	 * 计算node节点的BF值	 * @param node	 * @return	 */	public int calcNodeBalanceValue(AVLNode node) {
    		if(node != null) {
    			return getHeightByNode(node);		}		return 0;	}		private int getHeightByNode(AVLNode node) {
    		if(node == null) {
    			return 0;		}		return getChildDepth(node.leftChild) - getChildDepth(node.rightChild);	}		private int getChildDepth(AVLNode node) {
    		if(node == null) {
    			return 0;		}		return 1 + Math.max(getChildDepth(node.leftChild), getChildDepth(node.rightChild));	}			/**	 * 中序遍历	 */	public void middOrderErgodic() {
    		this.middOrderErgodic(this.root);	}	public void middOrderErgodic(AVLNode node) {
    		if(node != null) {
    			this.middOrderErgodic(node.leftChild);			System.out.print(node.data + ", ");			this.middOrderErgodic(node.rightChild);		}	}			/**	 * 删除指定val值的节点	 * @param val	 * @return	 */	public boolean delete(int val) {
    		AVLNode node = getNode(val);		if(node == null) {
    			return false;		}		boolean flag = false;		AVLNode p = null;		AVLNode parent = node.parent;		AVLNode leftChild = node.leftChild;		AVLNode rightChild = node.rightChild;		if(leftChild == null && rightChild == null) {
    			if(parent != null) {
    				if(parent.leftChild == node) {
    					parent.leftChild = null;				}				else if(parent.rightChild == node) {
    					parent.rightChild = null;				}			}			else {
    				this.root = null;			}						p = parent;			node = null;			flag = true;		}		else if(leftChild == null && rightChild != null) {
    			if(parent != null && parent.data > val) {
    				parent.leftChild = rightChild;			}			else if(parent != null && parent.data < val) {
    				parent.rightChild = rightChild;			}			else {
    				this.root = rightChild;			}			p = parent;			node = null;			flag = true;		}		else if(leftChild != null && rightChild == null) {
    			if(parent != null &&  parent.data > val) {
    				parent.leftChild = leftChild;			}			else if(parent != null && parent.data < val) {
    				parent.rightChild = leftChild;			}			else {
    				this.root = leftChild;			}						p = parent;			node = null;			flag = true;		}		else if(leftChild != null && rightChild != null) {
    			AVLNode successor = getSuccessor(node);			int tempData = successor.data;			if(delete(tempData)) {
    				node.data = tempData;			}			p = successor;			successor = null;			flag = true;		}				if(flag) {
    			this.rebuild(p);		}		return flag;		}			/**	 * 获得指定节点	 * @param key	 * @return	 */	public AVLNode getNode(int key) {
    			AVLNode node = root;		int t;		do {
    			t = node.data - key;			if(t > 0) {
    				node = node.leftChild;			}			else if(t < 0) {
    				node = node.rightChild;			}			else {
    				return node;			}		} while(node != null);		return null;	}			/***	 * 获得指定节点的后继	 * 找到node节点的后继节点     * 1、先判断该节点有没有右子树，如果有，则从右节点的左子树中寻找后继节点，没有则进行下一步     * 2、查找该节点的父节点，若该父节点的右节点等于该节点，则继续寻找父节点，     *   直至父节点为Null或找到不等于该节点的右节点。     * 理由，后继节点一定比该节点大，若存在右子树，则后继节点一定存在右子树中，这是第一步的理由     *      若不存在右子树，则也可能存在该节点的某个祖父节点(即该节点的父节点，或更上层父节点)的右子树中，     *      对其迭代查找，若有，则返回该节点，没有则返回null	 * @param node	 * @return	 */	public AVLNode getSuccessor(AVLNode node) {
    		if(node.rightChild != null) {
    			AVLNode rightChild=  node.rightChild;			while(rightChild.leftChild != null) {
    				rightChild = rightChild.leftChild;			}			return rightChild;		}		AVLNode parent = node.parent;		while(parent != null && (node == parent.rightChild)) {
    			node = parent;			parent = parent.parent;		}		return parent;	}			/**	 * 层序遍历	 */	public void sequenceErgodic() {
    		if(this.root == null) {
    			return;		}		Queue
    
      queue = new LinkedList<>();		AVLNode temp = null;		queue.add(this.root);		while(!queue.isEmpty()) {
    			temp = queue.poll();			System.out.println("当前节点值：" + temp.data + ", BF：" + calcNodeBalanceValue(temp));			if(temp.leftChild != null) {
    				queue.add(temp.leftChild);			}			if(temp.rightChild != null) {
    				queue.add(temp.rightChild);			}		}	}		public static void main(String[] args) {
    		MyAVLTree bbt = new MyAVLTree();        bbt.put(3);        bbt.put(2);        bbt.put(1);        bbt.put(4);        bbt.put(5);        bbt.put(6);        bbt.put(7);        bbt.put(10);        bbt.put(9);        bbt.middOrderErgodic();        System.out.println();        System.out.println("-----各节点平衡状况-----");        bbt.sequenceErgodic();        System.out.println();        bbt.delete(5);        bbt.delete(2);        bbt.middOrderErgodic();        System.out.println();        System.out.println("-----各节点平衡状况-----");        bbt.sequenceErgodic();        System.out.println();        	}}
参考：

《大话数据结构》

转载于:https://www.cnblogs.com/lishanlei/p/10707794.html

你可能感兴趣的文章
敏捷开发中软件测试团队的职责和产出是什么？
查看>>
在mvc3中使用ffmpeg对上传视频进行截图和转换格式
查看>>
python的字符串内建函数
查看>>
Spring - DI
查看>>
微软自己的官网介绍 SSL 参数相关
查看>>
Composite UI Application Block (CAB) 概念和术语
查看>>
ajax跨域，携带cookie
查看>>
阶段3 2.Spring_01.Spring框架简介_03.spring概述
查看>>
阶段3 2.Spring_02.程序间耦合_1 编写jdbc的工程代码用于分析程序的耦合
查看>>
阶段3 2.Spring_01.Spring框架简介_04.spring发展历程
查看>>
阶段3 2.Spring_02.程序间耦合_3 程序的耦合和解耦的思路分析1
查看>>
阶段3 2.Spring_02.程序间耦合_5 编写工厂类和配置文件
查看>>
阶段3 2.Spring_01.Spring框架简介_05.spring的优势
查看>>
阶段3 2.Spring_02.程序间耦合_7 分析工厂模式中的问题并改造
查看>>
阶段3 2.Spring_02.程序间耦合_4 曾经代码中的问题分析
查看>>
阶段3 2.Spring_03.Spring的 IOC 和 DI_2 spring中的Ioc前期准备
查看>>
阶段3 2.Spring_03.Spring的 IOC 和 DI_4 ApplicationContext的三个实现类
查看>>
阶段3 2.Spring_02.程序间耦合_8 工厂模式解耦的升级版
查看>>
阶段3 2.Spring_03.Spring的 IOC 和 DI_6 spring中bean的细节之三种创建Bean对象的方式
查看>>
阶段3 2.Spring_04.Spring的常用注解_2 常用IOC注解按照作用分类
查看>>
喝酒易醉，品茶养心，人生如梦，品茶悟道，何以解忧？唯有杜康！-- 愿君每日到此一游！
当前时间: 2024-10-07 14:21:56   当前IP: 3.145.18.101   联系邮箱:javaeecc@qq.com     Copyright © 2020 - 2022 baihongyu.com 京ICP备2021015314号-2
强烈建议你试试无所不能的CHAT-GPT，快点击我
强烈建议你试试无所不能的CHAT-GPT，快点击我